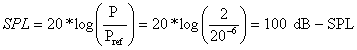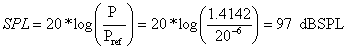|
Suma de Presiones Sonoras, una posición Institucional InstitucionalRoger Aguirre e-mail: [email protected] |
|||
| Algunas calculadoras:
Con las herramientas de cálculos con que contamos en la actualidad y los desarrollos alcanzados con los line array, lo ideal es obtener de nuestro sistema un sistema coherente y correlacionado, no obstante siempre vamos a encontrarnos que por alguna u otra razón o circunstancia nuestro sistema se va a comportar como un sistema no coherente y de fase aleatoria…
Con un poco de paciencia y dedicación podrán encontrar, a través del Internet, muchos tips, documentos y comentarios con respecto a este tema, sus vertientes e implicaciones.
Nota del Editor Yo pensaba hacer una presentación de mi exalumno Roger Aguirre, pero Roger me dejó sin palabras y sin espacio. Una investigación de este calibre merece un reconocimeinto institucional que voy a proponer al Consejo Académico de la Escuela. Un verdadero Ingeniero es el que con talento e ingenio puede construir un todo. Mis respetos. José Mujica |
Algunos conceptos importantes en este tema: "suma de fuentes coherentes y no coherentes", "presión sonora eficaz y presión sonora instantánea" Presión sonora eficazEn un punto, es la raíz cuadrada del valor medio, durante un ciclo, del cuadrado de las presiones acústicas instantáneas en el punto considerado. La duración de la medida debe ser mayor si se trata de presiones no periódicas. Presión sonora instantáneaEn un punto, es la presión instantánea total en dicho punto, menos la presión estática. En cualquiera de los casos, fuentes coherente o no coherente a modo general y sabiendo que la definición matemática de presión sonora está representada en la siguiente ecuación:
Cuando tenemos dos fuentes, la variable presión sonora será siempre medida como el valor cuadrático medio (RMS), es decir;
donde en el tercer término de la ecuación tenemos; suma de dos fuentes coherentes y correlacionadas Dos fuentes produciendo la misma señal con idéntica fase, alineadas en tiempo, misma amplitud etc, análisis que se aplica para cualquier señal; ruido blanco, ruido rosa, música en mono aural (tono puro), responden a la ecuación:
Ejemplo: Dos altavoces con la misma señal de excitación, es decir fuentes coherentes y correlacionadas en: fase, tiempo, etc., radiando cada una 94 dB SPL (1 pascal). Bajo esta consideración y de acuerdo a la ecuación anterior, la presión total será:
es decir que:
aplicando raíz cuadrada en ambos términos de la ecuación nos queda que:
por lo que la presión resultante de esta dos fuentes coherentes y correlacionadas viene dada por la ecuación:
suma de dos fuentes no coherentes y no correlacionadas Dos altavoces reproduciendo cada uno una señal diferente, también llamado fase aleatoria (pueden ser dos senoidales no armónicas o defasadas o algún pasaje de |
Música de tipo estereofónica),
bajo estas condiciones tendremos dos fuentes no coherentes y no correlacionadas.
Bajo esta consideración la presión total será:
Nota: en este caso el tercer término de la ecuación es igual a cero al no estar correlacionadas las fuentes. Como ejemplo podemos tomar los valores antes utilizados, donde teníamos 2 altavoces radiando cada uno una presión de 94 dB SPL (1 Pascal), la señal de audio que los excita es un pasaje estereofónico, es decir no están correlacionados. Bajo esta consideración la presión total estará determinada por la siguiente ecuación:
sustituyendo los valores tenemos que:
aplicando raíz cuadrada en ambos términos de la ecuación nos queda que:
por lo que la presión resultante de esta dos fuentes no coherentes y no correlacionadas viene dada por la ecuación:
Este ultimo caso, donde la suma de dos presiones sonoras iguales da como resultado un incremento de +3dB, es el que por norma general se utiliza en muchas de las calculadoras de suma de presiones que encontramos en Internet, así como también en software de predicción acústica, donde lo que es tomado en cuenta como parámetros prácticos y ceñidos a la realidad son aquellos que a decir verdad nos encontramos en nuestro medio, es decir; fuentes estereofónicas, diversos puntos de escucha, retardo de señal por circuitos electrónicos, reflexiones, etc., en fin, fuentes no coherentes y no correlacionadas. Estos resultados pueden ser obtenidos por otros medio de otras ecuaciones, pero nos llevan a los mismos resultados. Lo importante es tener en cuenta que consideraciones estamos tomando en nuestro sistema para realizar los cálculos. Apoyado en el concepto "de que al sumar dos fuentes de audio iguales obtenemos un incremento de +3dB", he planificado mis trabajos sabiendo que la solución al incremento de nivel presión sonora no está en duplicar o cuadriplicar las cantidad de parlantes si no utilizar parlantes de mayor eficiencia. Durante la búsqueda y lectura encontré que; existe una divergencia importante a nivel de literatura y foros de intercambio, con respecto a este tema. Con el auge de los sistemas de arreglos lineales (line array) y los estudios realizados en este tipo de configuración, donde por optimización de diseños de cajas, mayor control sobre el frente de onda, resonancias, cancelación de frecuencias, etc., además de software de análisis de alta precisión como lo son el Smaart, SIM, Spectralab, Spectafoo, etc., y cada uno de los software de predicción acústica proporcionados por cada una de las marcas que actualmente desarrolla el mercado de los line array , se pueden obtener resultados óptimos del conjunto en situaciones puntuales y controladas, y es de esta manera que se están manejando valores diferentes en cuanto a los resultados tradicionales obtenidos en los cálculos de presión sonora. |
||
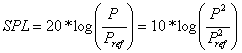 , donde,
, donde,